Számítógépes modellek fizikaórákon való használatában szerzett tapasztalat

Alekszandr Fedorovics Kavtrev , a fizika és a matematika kandidátusa Tudományok, Soros tanár, a Központ laboratóriumának vezetője Információs kultúra Szentpétervár

Az utóbbi időben gyakran hallani kérdéseket: "Szükség van-e számítógépre a fizikaórákon? A számítógépes szimulációk kiszorítják a valódi kísérleteket az oktatási folyamatból?" Az ilyen kérdéseket leggyakrabban olyan tanárok teszik fel, akik nem ismerik az információs technológiát, és nem igazán értik, hogy ezek a technológiák hogyan lehetnek hasznosak a tanításban.

Próbáljunk meg válaszolni a kérdésre: "Mikor indokolt a számítógépes programok használata a fizika órákon?" Úgy gondoljuk, hogy mindenekelőtt azokban az esetekben, amelyekben jelentős előny van a hagyományos képzési formákhoz képest. Az egyik ilyen eset a számítógépes modellek alkalmazása az oktatási folyamatban. Meg kell jegyezni, hogy a számítógépes modelleken a szerző olyan számítógépes programokat ért, amelyek lehetővé teszik fizikai jelenségek, kísérletek vagy problémák során felmerülő idealizált helyzetek szimulálását.

Mi az előnye a számítógépes modellezésnek a természetes kísérletekhez képest? A számítógépes modellezés mindenekelőtt lehetővé teszi a fizikai kísérletek és jelenségek vizuális dinamikus illusztrációinak megszerzését, azok finom részleteinek reprodukálását, amelyek a valós jelenségek, kísérletek megfigyelésekor gyakran megszöknek. A modellek használatakor a számítógép egyedülálló, valós fizikai kísérletben elérhetetlen lehetőséget ad arra, hogy ne egy valódi természeti jelenséget, hanem annak leegyszerűsített modelljét jelenítsük meg. Ebben az esetben fokozatosan további tényezők is bevonhatók a mérlegelésbe, amelyek fokozatosan bonyolítják a modellt, és közelebb hozzák a valós fizikai jelenséghez. Ezenkívül a számítógépes modellezés lehetővé teszi az események időskálájának változtatását, valamint olyan helyzetek szimulálását, amelyek nem valósulnak meg a fizikai kísérletekben.

A hallgatók számítógépes modellekkel végzett munkája rendkívül hasznos, mivel a számítógépes modellek lehetővé teszik a fizikai kísérletek kezdeti feltételeinek széles körű megváltoztatását, ami lehetővé teszi számos virtuális kísérlet elvégzését. Az ilyen interaktivitás óriási kognitív lehetőségeket nyit meg a hallgatók előtt, nem csak megfigyelőivé, hanem aktív résztvevőivé is teszi őket a lefolytatott kísérletekben. Egyes modellek lehetővé teszik a megfelelő grafikus függőségek felépítésének megfigyelését a kísérletek előrehaladásával egyidejűleg, ami növeli az egyértelműséget. Az ilyen modellek különösen értékesek, mert a tanulóknak jellemzően jelentős nehézségeik vannak a grafikonok felépítése és olvasása során.

Természetesen egy számítógépes laboratórium nem helyettesítheti a valódi fizikai laboratóriumot. Azonban teljesítő számítógép laboratóriumi munka bizonyos készségeket igényel, amelyek egy valódi kísérletre is jellemzőek - kezdeti feltételek kiválasztása, kísérleti paraméterek beállítása stb.

Az iskolai fizika tanfolyamon számos számítógépes modell található a cég által kifejlesztett multimédiás kurzusokban. Physicon ": "Physics in Pictures", "Open Physics 1.1", "Open Physics 2.0", "Open Astronomy 2.0" és "Open Chemistry 2.0". Ezek fő megkülönböztető jellemzője számítógépes tanfolyamok számtalan számítógépes modell – egyedi és eredeti fejlesztések, amelyeket sok országban nagyra értékelnek a felhasználók. (Ne feledje, hogy jelentős számú modell található az Open College honlapján is: http://www.college.ru/).

A Physikon cég által kifejlesztett számítógépes modellek könnyen illeszkednek az órába, és lehetővé teszik a tanár számára, hogy új, nem hagyományos oktatási tevékenységeket szervezzen a diákok számára. Íme három példa az ilyen tevékenységekre:

1. Problémamegoldó óra, majd számítógépes teszt. A tanár egyéni feladatokat ajánl fel a tanulóknak tanórán vagy házi feladatként önálló megoldásra, melyek helyességét számítógépes kísérletekkel ellenőrizhetik. A kapott eredmények független, számítógépes kísérlettel történő ellenőrzése növeli a tanulók kognitív érdeklődését, emellett kreatívvá teszi munkájukat, és gyakran természetében is közelebb hozza a tudományos kutatáshoz. Ennek eredményeként sok diák elkezd saját problémáival előállni, megoldani azokat, majd számítógépes modellek segítségével ellenőrzi érvelésének helyességét. A tanár tudatosan ösztönözheti a tanulókat ilyen tevékenységekre, anélkül, hogy félne attól, hogy egy rakás, a diákok által kitalált feladatot kell megoldania, amire általában nem jut elég idő. Sőt, az iskolások által összeállított feladatok felhasználhatók az órai munkában, vagy felajánlhatók más tanulóknak önálló tanulásra házi feladat formájában.
2. Lecke - kutatás. A tanulókat arra ösztönzik, hogy önállóan végezzenek egy kis tanulmányt számítógépes modell segítségével, és szerezzék meg a szükséges eredményeket. Ezenkívül sok modell lehetővé teszi, hogy szó szerint percek alatt elvégezzen egy ilyen vizsgálatot. Természetesen a tanár segíti a tanulókat a tervezés és a kísérletezés szakaszában.
3. Óra - számítógépes laboratóriumi munka. Egy ilyen lecke lebonyolításához megfelelő segédanyagokat kell kidolgozni. A laboratóriumi munkaformákban a feladatokat a bonyolultabbá váló sorrendbe kell rendezni. Eleinte célszerű egyszerű bevezető és kísérleti feladatokat, majd számítási feladatokat, végül kreatív és kutató feladatokat kínálni. Kérdés megválaszolásakor, feladatmegoldáskor a tanuló elvégezheti a szükséges számítógépes kísérletet és tesztelheti elképzeléseit. Javasoljuk, hogy a számítási feladatokat először hagyományos módon, papíron oldja meg, majd végezzen számítógépes kísérletet a kapott válasz helyességének ellenőrzésére. Vegyük észre, hogy a kreatív és kutatói feladatok jelentősen növelik a hallgatók érdeklődését a fizika iránt, és további motiváló tényezőt jelentenek. Emiatt az utóbbi két típus órái közelebb állnak az ideálishoz, hiszen a tanulók az önálló alkotómunka során szereznek ismereteket, mert tudásra van szükségük a számítógép képernyőjén látható konkrét eredmény eléréséhez. A tanár ezekben az esetekben csak asszisztens az ismeretszerzés kreatív folyamatában.

Interaktív számítógépes modellek alkalmazása az iskolások motivációjának növelésére a fizika tanulmányozása során.

Tapasztalataim szerint a modern számítástechnikai technológiákat és interaktív modelleket a hagyományos tanítási módszerekkel együtt alkalmazom a fizika tanulási motivációjának növelésére.
A fizika iskolai oktatása magában foglalja a tanfolyam folyamatos demonstrációs kísérletekkel való kísérését. Azonban in modern iskola A fizika kísérleti munkáinak elvégzése gyakran nehézséget okoz a tanítási idő hiánya és a korszerű tárgyi és technikai eszközök hiánya miatt. Az adventtel számítógép tartozék lehetővé vált a fizika tantárgy kísérleti részének kiegészítése és az órák eredményességének jelentős növelése. A számítógépek használata a fizika órákon valódi alkotói folyamattá varázsolja azokat, és lehetővé teszi a fejlesztő tanulás alapelvei megvalósítását. Lehetőség van a szükséges anyag kiválasztására, világos, áttekinthető és hozzáférhető módon történő bemutatására.
Használata során elkülönítheti a fő dolgot egy jelenségben, levághatja a kisebb tényezőket, azonosíthatja a mintákat, ismételten teszteket végezhet változó paraméterekkel, elmentheti az eredményeket, és megfelelő időben visszatérhet a kutatáshoz. Ezenkívül a számítógépes verzióban jelentősen elvégezhető nagy mennyiség kísérletek. Ez a típus A kísérletet egy adott törvény, jelenség, folyamat stb. számítógépes modelljével valósítják meg. A modellekkel való munka óriási kognitív lehetőségeket nyit meg a diákok előtt, így nemcsak megfigyelők, hanem kísérletek aktív résztvevői is.
Az interaktív tréning felhasználása:
A számítógépes modellek olyan programok, amelyek lehetővé teszik fizikai jelenségek, kísérletek vagy idealizált helyzetek szimulálását a számítógép képernyőjén felmerülő problémák során.
A virtuális laboratóriumok összetettebb számítógépes programok, amelyek lényegesen többet nyújtanak a felhasználónak bőséges lehetőséget mint a számítógépes modellek.
A hallgatók számítógépes modellekkel, laboratóriumokkal végzett munkája rendkívül hasznos, hiszen számtalan virtuális kísérletet végezhetnek, sőt akár kisebb méretű kutatásokat is végezhetnek. Az interaktivitás óriási kognitív lehetőségeket nyit meg a tanulók előtt, így nem csak megfigyelők, hanem aktív résztvevők is a folyamatban lévő kísérletekben.
Mivel az interaktív tanulás a legmodernebb tanulás, ezért egy hipotézist állítunk fel: a modern használatával számítógépes technológia Erősíteni kell az iskolások motivációját a fizika tanulására. Hiszen a motiváció kialakulásának szintje az fontos mutató az oktatási folyamat hatékonysága. Használat modern technológiák amikor a fizika tanulmányozása segít megoldani ezt a problémát.
2003 óta használom a modern információs technológiákat tanítási órákon és tanítás után, és a korszerű számítástechnikai eszközök és az iskolai internetkapcsolatok megjelenésével tovább bővültek a 21. század színvonalának megfelelő fizikaóra szervezésének és lebonyolításának lehetőségei. . Tanóráim során egyre inkább igyekszem interaktív fizikai kísérleteket, kutatásokat és laboratóriumi oktatási tevékenységformákat alkalmazni.
Az iskolások motivációjának növelésének eszközei a fizika tanulmányozása során
A következő munkaformákat tartom szem előtt:
lecke, problémahelyzet kialakításával annak különböző szakaszaiban;
számítógépes tesztelés használata;
tanórán kívüli munka projektek és kutatások végrehajtására internetes források és képzési programok segítségével.
Az alábbi oktatási módszereket használom:
- elméleti: a kutatási probléma pedagógiai, módszertani és szakirodalmának elemzése;
- általános tudományos: pedagógiai megfigyelés, beszélgetések iskolásokkal, tanulói teljesítmények elemzése, a fizika iskolai oktatására szánt számítógépes szoftvertermékek tanulmányozása, az információs technológiai eszközök iskolások oktatásában való használatának tapasztalatainak tanulmányozása és elemzése;
- statisztikai: a tanítási tapasztalatok eredményeinek feldolgozása.
A tanár feladata éppen az, hogy biztosítsa az oktatási és kognitív tevékenység motívumainak megjelenését, megőrzését és túlsúlyát.
Kezdjük egy olyan ösztönzővel, mint az oktatási anyagok újszerűsége és a kognitív tevékenység jellege. Az újnak a tanult régien kell alapulnia. Az óra elején az iskolások tudásának frissítése érdekében fizikai diktálást végzek, egyre inkább multimédiás termékeket használva.
A tanulókkal végzett munka megszervezésének fő módszerei a beszélgetés, a megfigyelés, a tapasztalatszerzés és a gyakorlati munka, amelyben túlsúlyban van a tanulók kognitív tevékenységének heurisztikus jellege. Ezek a módszerek biztosítják a kutatási készségek és képességek fejlesztését, megtanítják őket önálló döntéshozatalra.
Az oktatási tevékenység fő formája a tanóra, melyen reproduktív, tréning és végső megerősítés, valamint elméleti felmérés segítségével igyekszem minden tanuló számára sikerhelyzetet teremteni.
Munkám során a következő didaktikai elvekre támaszkodom:
a képzés individualizálása és differenciálása;
a kreativitás és a siker elve
bizalom és támogatás elve
a gyermekek társadalmi környezetük életébe való bevonásának elve.
A technológiai komponensnek (tanítási módszerek és technikák) véleményem szerint az alábbi követelményeknek kell megfelelnie:
párbeszédes;
aktív és kreatív karakter;
összpontosítani a gyermek egyéni fejlődésének támogatására;
biztosítja számára a szükséges teret az önálló döntések meghozatalához, a kreativitáshoz és a választáshoz.

Oktatási és Tudományos Minisztérium Krasznodar régió

Állami szakmai költségvetés oktatási intézmény Krasznodar régió

"Pashkovsky Mezőgazdasági Főiskola"

Módszertani fejlesztés

Fizikai kísérletek interaktív modelljeinek alkalmazása a fizika tanulmányozásában

Krasznodar 2015

EGYETÉRT

Helyettes igazgatója MR

GBPOU KK PSHK

ŐKET. Strotskaya

2015

Módszertani fejlesztést mérlegeltek a Központi Bizottság ülésén

matematikai és természettudományi tudományágak

A Központi Bizottság elnöke

_________________ (Pushkareva N.Ya.)

BEVEZETÉS

Az oktatás korszerűsítése az oktatási folyamat számítógépesítése terén kiterjeszti a tanulók önmegvalósításának lehetőségeit, rászoktatja őket az önkontrollra, jelentősen gazdagítja a képzés tartalmát, lehetővé teszi az egyénre szabott képzést. A számítógépes innovatív technológiák információorientációt biztosítanak az oktatási rendszer számára, felkészítve a tanulókat az új tevékenységi feltételekre információs környezet.

A dolgozat példát ad matematikai és fizikai ingák virtuális modelljeinek, egy síkon lévő blokknak és összekapcsolt testek rendszerének alkalmazására a harmonikus rezgések és a testmozgások tanulmányozásában több erő hatására. A szerző módszertani ajánlásokat ad ezek használatára a digitális források oktatási folyamatban történő hatékony felhasználása érdekében. Az ilyen innovatív technológia alkalmazása a műszaki szakterületeken különösen releváns, gyakorlatorientált képzéssel, amelyet a szakmai színvonal követelményei biztosítanak, és a leendő főiskolai végzettségűek további tevékenysége határoz meg.

A munka célja, hogy módszertani feltételeket biztosítson a fizika „Harmonikus rezgések” és „Dinamika” részeinek tanulmányozásához és oktatásához. kötelező használat interaktív rész.

– válassza ki és adaptálja az elméletet ebben a kérdésben a harmadik generációs szövetségi állami oktatási szabványok (FSES SPO) követelményeivel összhangban az „ODP 11. Fizika” tudományágra vonatkozóan;

Hatékonyan használja fel a bemutatott módszertani anyagokat az általános és legfőképpen a szakmai kompetenciák fejlesztésére;

– példát dolgozzon ki a modellek lehetséges alkalmazására előadásokon, gyakorlati és laboratóriumi órákon;

– óraterveket készíteni az interaktív modellekkel való munkavégzéshez;

– figyelembe kell venni a meglévő tapasztalatok felhasználásának sajátosságait a műszaki szakterület hallgatóival végzett foglalkozásokon:

08.02.01 „Épületek és építmények építése és üzemeltetése”; 08.02.07 „Belső vízvezeték-berendezések, légkondicionálás és szellőztetés szerelése és üzemeltetése”;

02/08/03 „Nem fém építőipari termékek és szerkezetek gyártása”;

04. 02. 21. „Földgazdálkodás”.

A fejlesztés a fizikai folyamatok számítógépes modelljeit használja, amelyeket N. E. Bogdanov készített. 2007-ben. Olyan virtuális konstruktorról van szó, amelynek célja a tanulás tevékenység-alapú megközelítése, ami különösen fontos a középszintű szakemberek szakmai képzésében. Főleg az építőipar területén, amelyhez különösen fontos a különböző típusú szerkezetek fizikai folyamatainak, egyensúlyi feltételeinek, szilárdsági határainak elemzése és megértése.

Ez a módszertani fejlesztés megfelel a fő szakember elsajátításának eredményeire vonatkozó követelményeknek oktatási program, mely szerint a technikusnak az alábbi általános és szakmai kompetenciákkal kell rendelkeznie:

OK 4. A szakmai feladatok elvégzéséhez szükséges információk keresése és felhasználása.

OK 5. Használja az információs és kommunikációs technológiákat szakmai tevékenység.

PC 1.4. Vegyen részt egy projekt kidolgozásában információs technológia felhasználásával végzett munka előállítására.

1 A kísérlet számítógépes szimulációja

A számítógépes modellezés mindenekelőtt lehetővé teszi a fizikai kísérletek és jelenségek vizuális dinamikus illusztrációinak megszerzését, azok finom részleteinek reprodukálását, amelyek az oktatási folyamat során valós jelenségek megfigyelésekor gyakran megszöknek. A modellek használatakor a számítógép egyedülálló lehetőséget biztosít arra, hogy a hallgató ne egy valódi természeti jelenséget, hanem annak leegyszerűsített modelljét jelenítse meg. Ugyanakkor a tanárnak lehetősége van arra, hogy fokozatosan olyan további tényezőket vegyen figyelembe, amelyek fokozatosan bonyolítják a modellt, és közelebb hozzák egy valós fizikai jelenséghez. Emellett a számítógépes modellezés lehetővé teszi az események időskálájának variálását, lépésről lépésre történő mérlegelését, és olyan helyzetek szimulálását is, amelyek fizikai kísérletekben nem valósíthatók meg.

A hallgatók interaktív modellekkel végzett munkája hasznos, hiszen a számítógépes modellek lehetővé teszik a fizikai kísérletek kezdeti feltételeinek széles körű megváltoztatását és számos virtuális kísérlet elvégzését. Hatalmas kognitív lehetőségek nyílnak meg a hallgatók előtt, amelyek lehetővé teszik számukra, hogy ne csak megfigyelői, hanem aktív résztvevői is legyenek a lefolytatott kísérleteknek. Egyes modellek lehetővé teszik a megfelelő grafikus függőségek felépítésének megfigyelését a kísérletek előrehaladtával egyidejűleg, ami növeli azok áttekinthetőségét. A tanárnak ezeknek a grafikus függőségeknek a megjelenésére kell összpontosítania, különösen a „Mechanikai rezgések” részben, ahol kényelmes bemutatni a tanulóknak az energiamegmaradás törvényének lényegét. Ebben a módszertani fejlesztésben ezt a pontot a 2.1.1. bekezdés tartalmazza. A 2. szakasz leírja a modellek használatát a tanári előadásokhoz az osztályteremben, vagy a hallgatók önálló munkájához olyan anyagokkal, amelyek lehetővé teszik számukra a száraz elmélet „újraélesztését”. A modell képernyőképei lehetővé teszik a fizikai mennyiségek változásának dinamikájának bemutatását.

A számítógéppel szimulált fizikai élmény megfigyelésekor és leírásakor a tanulónak:

határozza meg, hogy az élmény milyen fizikai jelenséget vagy folyamatot illusztrál;

nevezze meg a telepítés fő elemeit;

röviden írja le a kísérlet menetét és eredményeit;

javasolja, hogy mit lehet változtatni a telepítésben, és ez hogyan befolyásolja a kísérlet eredményeit;

levonni a következtetést.

Annak érdekében, hogy egy számítógépes óra ne csak formailag érdekes legyen, hanem a maximális oktatási hatást is kifejtse, a tanárnak előzetesen tervet kell készítenie a tanuláshoz választott számítógépes modellel való munkavégzésre, kérdéseket és feladatokat kell megfogalmaznia, amelyekkel egyeztetett. funkcionalitás modellnél arra is tanácsos figyelmeztetni a tanulókat, hogy az óra végén kérdésekre kell válaszolniuk, vagy rövid beszámolót kell írniuk az elvégzett munkáról. A szerző jelen mellékletekben fejlesztő óravázlatokat, önálló tantermi feladatokat, ill házi feladat, teszt a tudás ellenőrzésére.

Az egyéni feladatok egyik típusa a tesztfeladatok, amelyeket számítógépes ellenőrzés követ. Az óra elején a tanár egyéni nyomtatott feladatokat oszt ki a tanulóknak, és felkéri őket a feladatok önálló megoldására akár az órán, akár házi feladatként. A tanulók segítségével ellenőrizhetik a problémamegoldás helyességét számítógépes program. A virtuális kísérletben elért eredmények önálló utólagos ellenőrzésének lehetősége fokozza a kognitív érdeklődést, kreatívvá teszi a tanulók munkáját, természetében közelebb hozhatja a tudományos kutatáshoz.

Van még egy pozitív tényező a számítógépes kísérletek alkalmazása mellett. A technológia arra ösztönzi a tanulókat, hogy alkossanak saját problémáikat, majd interaktív modellek segítségével teszteljék érvelésüket.

A tanár felkérheti a tanulókat, hogy vegyenek részt ilyen tevékenységekben, anélkül, hogy félnének attól, hogy a későbbiekben ellenőriznie kell egy csomó problémát, amit kitaláltak. Az ilyen feladatok hasznosak, mivel lehetővé teszik a tanulók számára, hogy lássanak élő kapcsolat számítógépes kísérlet és a vizsgált jelenségek fizikája. Sőt, a tanulók által összeállított feladatok felhasználhatók az órai munkában, vagy házi feladat formájában felajánlhatók más tanulóknak önálló tanulásra.

1.1 Az elektronikus média használatának előnyei és hátrányai

a folyamatok láthatósága, a fizikai létesítmények és modellek tiszta, apró részletekkel nem zsúfolt képei;

a fizikai folyamatok és jelenségek többször megismételhetők, megállíthatók, visszagörgethetők, ami lehetővé teszi a tanár számára, hogy a tanulók figyelmét összpontosítsa, részletes magyarázatot adjon anélkül, hogy elsietné a kísérletet;

a rendszerparaméterek tetszőleges megváltoztatásának képessége, fizikai modellezés, hipotézisek felállítása és érvényességük ellenőrzése;

a folyamat szinkron fejlődését leíró grafikus függőségek beszerzése és elemzése;

használja az adatokat céljainak megfogalmazásához;

elméleti anyagra hivatkozni, történelmi hivatkozásokat tenni, a kivetítő képernyőjén megjelenő definíciókkal és törvényekkel dolgozni;

A használat hátrányai elektronikus eszközökkel kiképzés:

különböző formákban kódolt, sűrű információáramlás, amelyet a tanulóknak nem mindig van idejük feldolgozni;

Gyorsan beáll egyik-másik „megszokása”. szoftver termék, aminek következtében az érdeklődés intenzitása elvész;

a számítógép helyettesíti a tanárral való élő érzelmi kommunikációt;

a gyakornokoknak át kell váltaniuk a tanár szokásos hangjáról egy beszédhangra, gyakran rossz minőségű hanggal;

valamilyen show-elem jelenléte a gyakornokok számára, amikor inkább külső szemlélő, mint résztvevő szerepét töltik be a folyamatban.

Mind az előnyök, mind a hátrányok kiegészíthetők, vagy a számítógép használatának néhány negatív vonatkozása pozitívra fordítható. Például lefordítani a számítógépes modellezés használatának motivációs vonatkozásait oktatási tevékenységek a didaktikai játékok síkjára.

2Virtuális modellek használata a fizika tanulmányozásában

A következő részek felvázolják egy matematikai és fizikai inga virtuális modelljének használatát a harmonikus rezgések elméletének lényegének megértéséhez, valamint a csatolt testek és egy síkon lévő blokk modelljét a testek mozgásának vizsgálatakor. több erőből. Az alábbiakban példákat mutatunk be a középfokú műszaki hallgatókkal végzett munka során használható feladatokra oktatási intézmények.

2.1 Matematikai inga

2.1.1 Harmonikus rezgések és jellemzőik

Az oszcillációk olyan mozgások vagy folyamatok, amelyeket bizonyos időbeli megismételhetőség jellemez. Az oszcillációk széles körben elterjedtek a környező világban, és nagyon eltérő természetűek lehetnek. Ezek lehetnek mechanikus (inga), elektromágneses (oszcillációs áramkör) és más típusú rezgések. A szabad vagy természetes oszcillációk olyan rezgések, amelyek egy önmagára hagyott rendszerben fordulnak elő, miután azt külső hatás kimozdította az egyensúlyból. Példa erre egy menetre felfüggesztett golyó oszcillációja, 1. ábra.

1. ábra - Példa a legegyszerűbb oszcillációs folyamatra - egy golyó oszcillációjára a szálon

A rezgések legegyszerűbb fajtája - a harmonikus rezgések - különleges szerepet tölt be az oszcillációs folyamatokban. A felharmonikus rezgések képezik az alapját a különféle természetű rezgések vizsgálatának egységes megközelítésének, hiszen a természetben és a technikában fellelhető rezgések gyakran közel állnak a harmonikusokhoz, és az eltérő formájú periodikus folyamatok harmonikus rezgések szuperpozíciójaként ábrázolhatók.

A harmonikus rezgések azok a rezgések, amelyekben az oszcilláló mennyiség idővel a szinusz vagy koszinusz törvénye szerint változik.
A harmonikus rezgések egyenlete a következőképpen alakul:

ahol A az oszcillációk amplitúdója (a rendszer egyensúlyi helyzetétől való legnagyobb eltérésének nagysága); - körkörös (ciklikus) frekvencia. A koszinusz periodikusan változó argumentumát oszcillációs fázisnak nevezzük. Az oszcilláció fázisa határozza meg az oszcilláló mennyiség elmozdulását az egyensúlyi helyzetből. Ebben a pillanatban idő t. A φ konstans a fázisértéket jelenti t = 0 időpontban, és az oszcilláció kezdeti fázisának nevezzük. A kezdeti fázis értékét a referenciapont megválasztása határozza meg. Az x érték -A és +A közötti értékeket vehet fel.

Azt a T időtartamot, amelyen keresztül az oszcillációs rendszer bizonyos állapotai ismétlődnek, rezgésperiódusnak nevezzük. A koszinusz 2π periódusú periodikus függvény, ezért a T időtartam alatt, amely után az oszcillációs fázis 2π-nek megfelelő növekményt kap, a harmonikus rezgéseket végző rendszer állapota megismétlődik. Ezt a T időtartamot harmonikus rezgések periódusának nevezzük.

A harmonikus rezgések periódusa egyenlő: T = 2π/.

Az egységnyi idő alatti rezgések számát ν rezgési frekvenciának nevezzük.

A harmonikus rezgések frekvenciája egyenlő: ν = 1/T. A frekvencia mértékegysége a hertz (Hz) - másodpercenként egy rezgés.

A körfrekvencia = 2π/T = 2πν megadja a rezgések számát 2π másodpercben.

Grafikusan a harmonikus rezgések ábrázolhatók x t-től való függéseként, ésforgó amplitúdó módszer (vektordiagram módszer), amelyet az 1., 2. (A, B) ábra szemléltet.

2. ábra Grafikus kép oszcilláló mozgás koordinátákban ( x,t ) (A) és a vektordiagram módszer (B).

A forgó amplitúdó módszer lehetővé teszi a harmonikus rezgési egyenletben szereplő összes paraméter megjelenítését. Valójában, ha az A amplitúdóvektor φ szöget zár be az x tengellyel (lásd a 2. B ábrát), akkor a vetülete az x tengelyre egyenlő lesz: x = Acos(φ). A φ szög a kezdeti fázis. Ha az A vektort a rezgések körfrekvenciájával megegyező szögsebességgel forgatjuk, akkor a vektor végének vetülete az x tengely mentén mozog és -A-tól +A-ig terjedő értékeket vesz fel, és a koordináta ennek a vetületnek a törvény szerint idővel változni fog: . Ezt a 3. ábra (A-D) szemlélteti részletesen.

Így a vektor hossza megegyezik a harmonikus rezgés amplitúdójával, a vektor iránya a kezdeti pillanatban az x tengellyel szöget zár be, amely megegyezik a φ rezgések kezdeti fázisával, és az irányszög változása az idővel egyenlő a harmonikus rezgések fázisával. Az az idő, amely alatt az amplitúdóvektor egy teljes fordulatot tesz, megegyezik a harmonikus rezgések T periódusával. A vektorfordulatok száma másodpercenként megegyezik a ν rezgési frekvenciával.

3. ábra - Az oszcillációs mozgás grafikonjai a rezgés fázisától függően: 0,5π (A), π (B), 1,5π (C), 2π (D).

2.1.2 Csillapított harmonikus rezgések

Minden valós oszcillációs rendszerben vannak ellenállási erők, amelyek hatása a rendszer energiájának csökkenéséhez vezet. Ha az energiaveszteséget a külső erők munkája nem pótolja, a rezgések elhalnak. Az ilyen rezgéseket csillapítottnak nevezzük. A matematikai inga interaktív modelljében megadott oszcillációk mozgásegyenleteinek levezetését és megoldását a 4A, B ábra mutatja. Vizsgáljuk meg ezeket részletesebben.

A legegyszerűbb és egyben leggyakoribb esetben az ellenállási erő arányos a sebességgel:
, ahol r az ellenállási együtthatónak nevezett állandó érték. A mínusz jel annak a ténynek köszönhető, hogy az erő és a sebesség ellentétes irányú; ezért az X tengelyre vetületeik eltérő előjelűek. Figyelembe véve a helyreállító erő nagyságát
. Newton második törvényének egyenlete ellenállási erők jelenlétében a következőképpen alakul:
vagy
, ami egy másodrendű differenciálegyenlet.

4. ábra - Rezgési egyenletek levezetése (A) és rezgésegyenletek megoldása (B)

Így a mozgásegyenlet alakot ölt

A kifejezések átvitele jobbról balra, az egyenlet elosztása m-rel és jelölés
formában kapunk egyenletet

Ahol - a rendszer szabad oszcillációinak gyakorisága környezeti ellenállás hiányában (a rendszer természetes frekvenciája). Együttható
, amely az oszcillációk csillapítási sebességét jellemzi, csillapítási együtthatónak nevezzük.

Az interaktív modell jól szemlélteti a csillapítási együttható értékét. A 6. AB ábra jól szemlélteti, hogyan néz ki egy matematikai inga sebességének és koordinátáinak grafikonja a paramétereitől (felfüggesztési hossz és elhajlási szög) és a megadott értéktől függően . A virtuális modellben is nyomon követhető, hogyan épül fel a fázisportré és annak lényege. Az ábrákon jól látható, hogy a csillapítási együttható n-szeres növekedésével a rezgések száma n-szeresére csökken.

5. ábra A, B - Példák csillapított oszcillációkra

7. ábra A, B – A rendszer főbb paramétereinek számításai

2.1.3 Harmonikus rezgések energiája

Az oszcillációs rendszer teljes mechanikai energiája megegyezik a mechanikai és a potenciális energiák összegével.

Különböztessük meg a kifejezést az idő függvényében
, kapunk

= = -a bűn(t + ).

A terhelés kinetikus energiája egyenlő

E =
.

A potenciális energiát a jól ismert képlet fejezi ki
x helyett
, kapunk

Mert
.

Teljes energia
az érték állandó. Az oszcilláció során a potenciális energia kinetikus energiává alakul és fordítva, de minden energia változatlan marad.

A 7. és 8. ábra jól szemlélteti a kinetikai és potenciális energia változásait a matematikai inga lengéseinek csillapítási együtthatója és csillapított rezgései esetén.

7. ábra - A harmonikus rezgések kinetikus és potenciális energiájának változásainak grafikonjai

8. ábra – A csillapított oszcillációk kinetikai és potenciális energiájának változásait ábrázoló grafikonok.

2.2 Fizikai inga

Fizikai inga minden olyan merev test, amely a gravitáció hatására képes oszcillálni egy rögzített vízszintes tengely körül, amely nem megy át a tömegközépponton.

9. ábra – Fizikai inga

Az inga az egyensúlyi helyzettől való kis eltérési szögben harmonikus rezgéseket hajt végre.

A fizikai inga harmonikus rezgésének periódusát az összefüggés határozza meg

Ahol

az inga tehetetlenségi nyomatéka a forgástengelyhez képest,

Inga tömege,

A felfüggesztési pont és a tömegközéppont közötti legrövidebb távolság,

A gravitáció gyorsulása.

Az inga forgástengelye nem megy át a súlypontján, így a tehetetlenségi nyomatékot Steiner tétele határozza meg:

Ahol

Egy test tehetetlenségi nyomatéka a tömegközépponton átmenő és az adott egységgel párhuzamos tengely körül. Ezt figyelembe véve átírjuk az időszak képletét:

A fizikai inga kis oszcillációinak periódusát néha a következő formában írják:

Ahol .

- a fizikai inga csökkentett hossza– egy olyan matematikai inga hosszával számszerűen megegyező mennyiség, amelynek rezgési periódusa egybeesik egy adott fizikai inga periódusával.

P Az ebben a munkában használt fizikai inga vékony, hosszúságú rúd alakúl . - gravitáció középpontja,- az a felfüggesztési pont, amelyen a forgástengely áthalad, merőlegesen a rajzra.

Amikor a prizma rögzítve van, a rúd az O vízszintes tengelyhez képest oszcillál, és a prizma alsó élével egy rögzített szilárd állványon nyugszik, amelyet egy állvány tart.

10. ábra – Fizikai diagram

inga

A felfüggesztési pontnak a rúd különböző pontjain történő rögzítésével megváltoztathatja a távolságot.

Egy egyenletes vékony rúd tehetetlenségi nyomatéka a tömegközépponton átmenő tengelyhez viszonyítva egyenlő

Hol a rúd tömege, ott a hossza.

Ha behelyettesítjük a tehetetlenségi nyomaték kifejezést a periódus képletébe, a következőt kapjuk:

. Akkor jelöljük .

Az oszcilláció periódusát kísérletileg úgy határozhatjuk meg, hogy stopperrel megmérjük azt az időt, amely alatt a rúd teljes oszcillációt végez.

Nézzük négyzetre, és kapjunk egy működő képletet a gravitációs gyorsulás kiszámításához:

(10).

2.3 Blokkolás ferde síkon

A modell egy virtuális kísérletet valósít meg, amelynek célja egy blokk ferde sík mentén történő mozgásának tanulmányozása száraz súrlódás és külső erő jelenlétében. A kísérlet végrehajtása során kiválasztható a μ súrlódási tényező, a blokk tömege m, sík dőlésszöge α. Különböző paraméterek esetén a relatív sebesség és idő grafikonja látható. A blokk ferde sík mentén történő elcsúsztatása csak akkor lehetséges, ha a statikus súrlódási erő eléri a maximális értékét ( F tr)max:

Ezeket az erőket általában csúszósúrlódási erőnek nevezik. Newton második törvénye határozza meg azt a gyorsulást, amelyet ilyen feltétel mellett a blokk ferde sík mentén elcsúszik.

Nál nél a < 0 брусок начинает двигаться вверх по наклонной плоскости (из-за наличия внешней силы). В этом случае сила трения скольжения изменяет знак на противоположный.

Ha nincs külső erő, akkor a sík maximális α max dőlésszöge, amelynél a blokkot a statikus súrlódási erő még mozdulatlanul tartja, az összefüggés határozza meg.

A gyakorlatban ezt az összefüggést használják a száraz súrlódási együttható mérésére.

Tekintsünk egy blokk virtuális modelljét ferde síkon a 11. ábrán. Közvetlenül a modellablak belsejében, a bal felső részben találhatók a „Start”, „Reset” és „Help” gombok. Amikor megnyomja a „Reset” gombot, a modell visszatér eredeti állapotába. Az ablak közepén a modell munkamezeje egy ferde sík képe és egy rajta csúszó blokk látható. A munkamező alatt van egy kijelző a súrlódási erő, a talajreakció erő, a testgyorsulás és a gravitációs vetület értékeivel. A sebességdiagram felett három vezérlő található. Segítségükkel megváltoztathatja a test síkbeli súrlódási együtthatóját, testtömegét és a sík dőlésszögét. Nézze meg alaposan a modellt, és találja meg az összes kezelőszervet.

11. ábra – Rúd egy síkon

Ezt a modellt kisegítő oktatási eszközként használhatjuk, amikor a „Test mozgása ferde síkban” témakörben tanítják a problémák megoldását.

2.4 Két test egy ferde síkban

12. ábra – Összekapcsolt testek ferde síkban

Rajzoljunk egy képet, és ábrázoljuk a rajta ható erőket. Feltételezzük, hogy a testek azonos a abszolút értékű gyorsulással mozognak, és a menet T feszültsége állandó a teljes hosszában.

Tegyük fel, hogy a jobb oldali súlyt leengedjük, a bal oldali pedig felemelkedik egy ferde sík mentén. A megfelelő súly két erő hatására mozog:

- gravitációs és menetfeszítő erő T 2.

A bal oldali teher egy ferde síkban mozog három erő hatására: m 1 g gravitáció, N támasztó reakcióerő és T 1 menetfeszítő erő. Vektor formában a mozgásegyenleteket rendszerként írjuk fel:

Vetítsük az első egyenletet X irányba a ferde sík mentén:

Vetítsük a rendszer második egyenletét az X függőleges irányra:

Vegyük észre, hogy bármely vektoregyenletet mindig két független irányba vetíthetünk. Ezt a két egyenletet összeadva (rendszert alkotnak), a következő kifejezést kapjuk:

Abból azt találjuk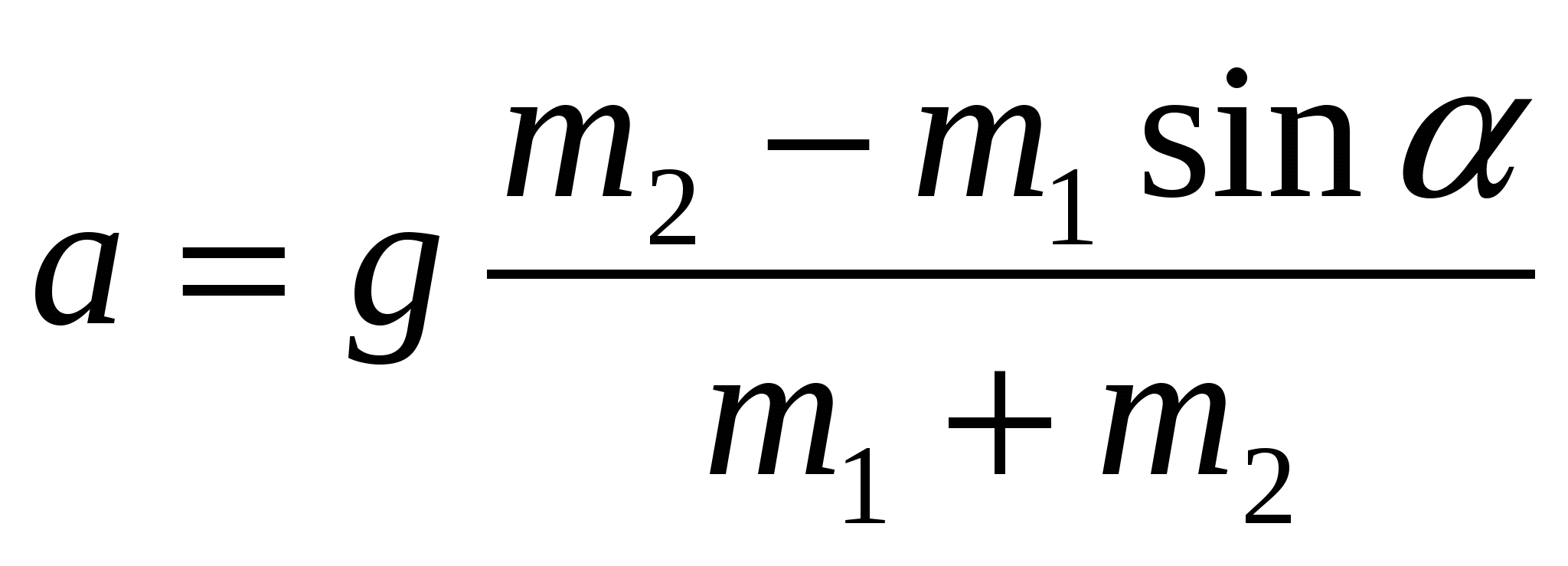

Látjuk, hogy ha m 1 sin α értéke nagyobb lenne m 2 -nél, akkor az a gyorsulás negatív értékké válna. Vagyis a rendszer az ellenkező irányba mozogna (m 1 rúd leengedve, m 2 terhelés megemelkedett). Az utolsó egyenletből megtaláljuk a menet feszítő erejét:

Tekintsünk most egy olyan rendszer virtuális modelljét, amely két összekapcsolt rúdból áll egy ferde síkon.

13. ábra – Összekapcsolt testek virtuális modellje

A munkamező jobb felső részén szabályozók találhatók, amelyekkel beállíthatja a rendszer paramétereit: terhelések tömege, dőlésszöge, súrlódási együtthatója. Az alábbiakban olyan információs ablakok találhatók, amelyek a gyorsulás, a súrlódási erő és a menetfeszültség számítási eredményeit mutatják.Vannak „Start”, „Reset” és „Súgó” gombok. Amikor megnyomja a „Reset” gombot, a modell visszatér eredeti állapotába. Az ablak közepén a modell munkamezeje egy ferde sík képe és egy rajta csúszó blokk látható. A „Súgó” gombra kattintva a tanuló olyan egyenleteket lát, amelyekkel önállóan számolhat ismeretlen mennyiségeket (14. ábra).

14. ábra – A csatlakoztatott karosszériamodell „Súgó” menüje

Ez a modell használható olyan problémák megoldására, amelyek összekapcsolt testek ferde síkban történő mozgásával kapcsolatosak. A függelék példákat ad azokra a problémákra, amelyek megoldásában ez a virtuális modell használható.

3 Gyakorlati gyakorlatok

A munka 2. szakasza a harmonikus rezgések elméletének alapjait és a ferde síktestek két gyakori esetét vizsgálta interaktív modellek illusztrációival. A 3. részben megnézzük, hogyan kell használni ezt a modellt virtuális laboratóriumként egy műszaki profilú középfokú szakképzési intézmény tanulóival való munkavégzés során gyakorlati órákon. A mechanikai rezgések tanulmányozására 8 órát szánnak, ebből 1 laboratóriumi munka a szabadesés gyorsulásának matematikai ingával történő kiszámításáról (2 óra).

A „Mechanikai rezgések” témakör tanulóinak asszimilációjának és megértésének ellenőrzésére lehetőség van egy matematikai inga virtuális modelljének használatára. A hallgatók egy ilyen modellt mutattak be annak érdekében, hogy egyértelműen bemutassák az oszcillációs folyamat alapelveit, valamint megfigyeljenek egy ilyen folyamatot.

3.1.1 Laboratóriumi feladat

Mint fentebb említettük, a „Mechanikai rezgések” témakör tanulmányozása laboratóriumi munka elvégzésével jár, amelynek oktatási és technológiai térképét a 2. függelék tartalmazza. A gyakorlati munkába való belépéshez vagy annak megvédéséhez egy matematikai inga interaktív modelljét használjuk. A 3. függelék határozza meg rövid utasításokat a táblázat kitöltésére a tanuló által a modellel végzett munka során szerzett kísérleti adatok alapján. Vannak olyan önkontroll kérdések is, amelyek segítenek a hallgatónak megvédeni munkáját. Egy ilyen integrált és átfogó megközelítés lehetővé teszi a tanár számára, hogy objektíven értékelje a tudást, és jelentősen időt takarítson meg, amelyet hatékonyabban használhat fel egyéni munkára és konzultációkra.

3.1.2 Hozzárendelés a matematikai ingamodellhez

A feladat a modell kezeléséhez szükséges utasításokat leíró bekezdéseket, a fő funkciók leírását és a grafikonokat tartalmazza. A 4. függelékben található. Segít a tanulónak megérteni a modell célját és elsajátítani beállításait. Ezen kívül a feladat tartalmaz tesztkérdéseket a „Mechanikai rezgések” témában és számos számítógépes kísérletet.

A bevezető feladatokban szereplő kísérletek lehetővé teszik, hogy mélyebben elmélyüljön a képernyőn zajló események jelentésében. A kísérletek elvégzéséhez elegendő ismerni a vizsgált téma alapképleteit. Az ilyen feladatok látszólagos egyszerűségük ellenére nagyon hasznosak, hiszen lehetővé teszik a hallgatók számára, hogy élő kapcsolatot lássanak a számítógépes kísérlet és a vizsgált jelenségek fizikája között.

A 4. függelék minden ismerkedési feladathoz egy válaszűrlapot is biztosít. A kapott válaszok űrlapon való rögzítése jelentősen csökkentheti a számítógépes modellel való munkavégzés idejét, és megkönnyíti a válaszok ellenőrzését.

3.1.3 „Mechanikai rezgések” teszt

A munka során elméleti tesztet alkalmaztunk „Mechanikai rezgések” témában (5. melléklet).

A tesztelés célja: a tanuló által az anyag elsajátítása során megszerzett ismeretek tesztelése.

A tesztkontroll nagyon fontos a pedagógiai folyamatban. Az ellenőrzés eredményétől függően születik döntés a további órák, konzultációk szükségességéről, a bukottak megsegítéséről. Az előkészítő tesztre adott válaszok az 5. számú mellékletben találhatók.

Ez a zárt típusú teszt kritérium-orientált, azaz a tesztelést az anyag elsajátítási fokának meghatározására és az eredmények összehasonlítására egy egyértelműen meghatározott teljesítményterülettel végzik.

A teszt 35 különböző nehézségű feladatból áll. A teszt céljától függően a tanár választhat bizonyos feladatokat.

3.1.4 „Mechanikai rezgések” és „Testek mozgása több erő hatására” leckék vázlata

Az 1. és 6. melléklet tartalmazza az előadási órákon használható órajegyzeteket.

3.1.5 Gyakorlatorientált feladatok

KÖVETKEZTETÉS

A meglévő tapasztalatok azt mutatják, hogy a leendő műszaki szakemberek szakmai kompetenciáinak fejlesztésében e módszertani ajánlás és a fizikai kísérletek virtuális modelljeinek alkalmazása hatékony.

A képzésben használt előadásokra és gyakorlati órákra generált feladatpéldák pozitív eredményeket hoztak. Hozzájárultak a tanuló tevékenységalapú tanulási szemléletének erősítéséhez, önfejlesztésre ösztönözték, többek között az informatika területén, valamint elmélyítették a természeti és ember által előidézett folyamatok fizikájával kapcsolatos ismereteit. Az is feltűnt, hogy e módszertani ajánlások alkalmazásakor a hallgatók edzik logikájukat, a felmerülő nehézségek arra késztetik őket, hogy önálló döntés feladatokat, mely közvetlenül hozzájárul a leendő technikus számára szükséges általános és szakmai kompetenciák kialakításához.

Az önkontroll feltételeit biztosító kérdéssor a hallgató számára lehetővé teszi a tudás köztes és végső ellenőrzésének objektív értékelését.

Befejezésül szeretném még egyszer hangsúlyozni az innovatív oktatási modellek és technológiák alkalmazásának fontosságát és szükségességét a középfokú szakoktatási intézmények hallgatóival való munka során. Mivel alkalmazásuk során kedvező feltételek teremtődtek a tanulás differenciálásához, individualizálásához.

A HASZNÁLT FORRÁSOK LISTÁJA

Avanesov V. S. Összetétel tesztfeladatokat/ V.S. Avanesov. – M.: Adept, 1998. – 191 p.

Boev V.D., Sypchenko R.P., Számítógépes modellezés / V.D. Boev, R.P. Szypcsenko. – M.: INTU IT.RU Kiadó, 2010. – 349 p.

Bulavin L.A., Vygornitsky N.V., Lebovka N.I. Számítógépes modellezés fizikai rendszerek/ L.A. Bulavin, N.V. Vigornickij – Dolgoprudnij: „Intelligencia” Kiadó, 2011. – 352 p.

Fizikatanárnak. Számítógép használata a fizika tanulmányozása során. - (Orosz). – URL: http://www. uroki. háló/ docfiz/ docfiz27. htm

Mayorov A. N. Iskolai teljesítménytesztek: tervezés, megvalósítás, használat. Oktatás és kultúra / A.N. Mayorov. – Szentpétervár: 1996. – 304 p.

Mayorov A.N. Az oktatási rendszer tesztjeinek létrehozásának elmélete és gyakorlata / A.N. Mayorov. – M.: „Hírszerző Központ”, 2001. – 296 p.

Minskin E.M. A játéktól a tudásig: kézikönyv tanároknak / Minskin E.M. – M.: Nevelés, 1982. – 192 p.

A tanulót fejlesztő fizika tanítása. 1. könyv. Megközelítések, összetevők, leckék, feladatok / Szerk. E. M. Braverman. – M.: Fizikatanárok Egyesülete, 2003. – 400 p..

Samoilenko P.I. Fizika társadalmi-gazdasági és humanitárius profilú szakmáknak: tankönyv középfokú szakemberek számára. oktatás / P.I. Samoilenko. – 6. kiadás, törölve. – M.: „Akadémia” Kiadói Központ, 2014. – 469 p.

Firsov A.V. Fizika a műszaki és természettudományi profilú szakmákhoz és szakterületekhez: tankönyv / A.V. Firsov; szerkesztette T. I. Trofimova. – 6. kiadás, törölve. – M.: „Akadémia” Kiadói Központ, 2014. – 352 p.

1. MELLÉKLET

Óraterv „Mechanikai rezgések”

2. MELLÉKLET

5. sz. laboratóriumi munka

A szabadesés gyorsulásának meghatározása inga segítségével.

A munka célja: Határozzuk meg a szabadesés gyorsulását az inga felfüggesztésen való lengési periódusának a felfüggesztés hosszától való függése alapján.

Megszerzett ismeretek és készségek:

Szabványos idő: 2 óra

Munkahelyi felszerelések: állvány csatlakozóval és lábbal, fonat hurkokkal a végén, súlykészlet, mérőszalag milliméteres osztással, elektronikus stopper

Rövid elmélet

P A matematikai inga periódusa a következő képletből határozható meg:

(1)

A periódusmérés pontosságának növelése érdekében meg kell mérni az inga maradék N számú teljes lengésének t idejét. Aztán pont

T=t/N (2)

A nehézségi gyorsulás pedig a képlet segítségével számítható ki

A munka befejezése:

1. Rögzítse a fület az állványrúd felső széléhez. Helyezze az állványt az asztalra úgy, hogy a láb vége túlnyúljon az asztal felületének szélén. Akassz egy súlyt a készletről a lábra. A rakománynak 3-4 cm-re kell lógnia a padlótól.

2. A mérések és számítások eredményeinek rögzítéséhez készítsen táblázatot:

Tapasztalat sz.

L, m

t, s

t átlag, s

T, s

g, m/s 2

3. Mérje meg szalaggal az L inga hosszát.
4. Készítse elő az időmérőt a stopper üzemmódban való működésre.
5. Hajtsa el az ingát 5-10 cm-rel és engedje el.
6. Mérje meg azt az időt t, amely alatt 40 teljes rezgést teljesít!
7. Ismételje meg a kísérletet 5-7 alkalommal, majd számítsa ki az átlagos időtartamot, amely alatt az inga 40 oszcillációt végez t avg.
8. Számítsa ki az oszcilláció periódusát a (2) képlet segítségével!
9. Számítsa ki a szabadesés gyorsulását a (3) képlet segítségével!
10. Határozza meg a kapott eredmény relatív hibáját:

* 100%, hol g változás – az elvégzett munka eredményeként számított gyorsulás nagysága,g– a referenciakönyvből vett érték.

Következtetés:

3. FÜGGELÉK

Feladat a matematikai ingamodellhez

A feladatok elvégzésekor használhatja a „Súgó” gombot.

Állítsa be a maximális elhajlási szöget.

Állítsa be az inga maximális hosszát.

Kattintson a "Start" gombra.

Négy teljes oszcilláció után nyomja meg a Stop gombot.

Felhívjuk figyelmét, hogy az oszcilláció folyamata során a potenciális energia mozgási energiává alakul, és fordítva. Ebben az esetben a teljes energia állandó marad.

Az ablak bal alsó sarkában egy rezgésszámláló és egy stopper található. Számítsa ki a rezgés periódusát kétféleképpen. Az első módszer kiszámításához használja a rezgések számát és a stopperórán látható időt. A másodikhoz használja a Thompson-képletet. Hasonlítsa össze az eredményeket.

A g gravitációs gyorsulás ehhez és az azt követő feladatokhoz 10 m/s 2 -nek számít. Az eredményeket kerekítse két tizedesjegyre. Rögzítse az eredményeket a válasz űrlapon.

Milyen feltételek mellett használható a Thompson-képlet?

Az oszcillációs periódus ismeretében számítsuk ki az ω 1 szögfrekvenciát.

Számítsa ki az ω 2 szögfrekvenciát az inga minimális hosszához!

Számítsa ki a lengés amplitúdóját az inga maximális és minimális hosszára!

Írjon megoldást az inga maximális és minimális hosszára vonatkozó rezgési egyenletre!

Kapcsolja ki a sebesség, kinetikai és potenciális energia grafikonokat.

Hasonlítsa össze az elmozdulás és az idő grafikonjait a maximális és minimális ingahosszra vonatkozóan.

Írja fel, hogy a rezgés fázisa mekkora növekményt kap a harmonikus rezgés periódusával megegyező idő alatt!

Számítsd ki a maximális sebességet egy 2,5 m hosszú inga és egy 1,25 m hosszúságú inga esetén.

Ellenőrizze számításait grafikusan. Ehhez kapcsolja ki az eltolási grafikont, és aktiválja a sebesség-idő grafikont. Hasonlítsa össze maximális sebességek különböző ingahosszúságokhoz grafikusan.

Számítsa ki a lengés maximális gyorsulását az inga maximális és minimális hosszára! Hasonlítsa össze az eredményeket.

Aktiválja az összes diagramot. Állítsa be az inga maximális hosszát és a maximális elhajlási szöget. Állítsa be a maximális csillapítás csökkentést is.

Kattintson a "Start" gombra.

Gondosan tanulmányozza az elmozdulás, a sebesség, a kinetikus és a potenciális energia grafikonját az idő függvényében és a fázisportrét.

Felhívjuk figyelmét, hogy az oszcilláció folyamata során a potenciális energia mozgási energiává alakul, és fordítva. Ebben az esetben az összenergia egy exponenciális törvény szerint csökken.

Számítsa ki az oszcilláció periódusát a Thompson-képlet segítségével!

Hasonlítsa össze a kapott rezgési periódust a kapott periódussal
7. bekezdés.

Az oszcillációs periódus ismeretében számítsuk ki az ω szögfrekvenciát!

Számítsa ki az oszcilláció maximális amplitúdóját!

Kattintson ismét a "Start" gombra. Egy teljes lendítés után nyomja meg a Stop gombot.

Számítsa ki a második rezgés maximális amplitúdóját a csillapítási együttható és az időzítő idő ismeretében.

Ellenőrizze számításait a „Számítás” gombra kattintva.

Írjon megoldást az inga maximális hosszára vonatkozó rezgési egyenletre!

Számítsa ki a sebesség és a gyorsulás maximális értékét az időzítő által megjelenített pillanatban.

Válasz űrlap a matematikai ingamodell feladatához
TELJES NÉV. tanuló ____________________________________________________________

4. FÜGGELÉK

Önálló munkavégzésre szóló megbízás

Az elkészült táblázatokat a tanulók a füzetükbe adják be laboratóriumi munkához. A kitöltéshez egy matematikai inga interaktív modelljét használjuk.

1 A) A csúszka 2-3 különböző pozícióba állításával az „Elhajlási szög” és az „Inga hossza” sorokban töltse ki a táblázatot. Ezzel egyidejűleg hagyja nullán a csúszkát a „Csillapítási együttható” sorban.

Elhajlási szög

Inga hossza

Időszak

Szögfrekvencia

Sebesség mx

Gyorsulás max

B) Keresse meg a kinetikus és a potenciális energia maximális értékét! Rajzolja fel az energia és az idő grafikonját!

B) Vonjon le következtetést a mechanikai rezgések típusáról!

2 A) A csúszka 2-3 különböző pozícióba állításával az „Elhajlási szög”, „Inga hossza” és „Csillapítási együttható” sorokban töltse ki a táblázatot.

Elhajlási szög

Inga hossza

Csillapítási együttható

Időszak

Szögfrekvencia

Sebesség mx

Gyorsulás max

B) Számítsa ki saját maga a feltüntetett értékeket, és hasonlítsa össze a számításokban megadottakkal. Adja meg a számításokat a füzetében, és rajzoljon egy fázisportrét.

Kérdések az önkontrollhoz:

Milyen rezgéseket nevezünk harmonikusnak? Mondjon példákat harmonikus rezgésekre!

Határozza meg a harmonikus rezgés következő jellemzőit: amplitúdó, fázis, kezdeti fázis, periódus, frekvencia, ciklikus frekvencia.

Vezesse le a harmonikus rezgések differenciálegyenletét, és írja fel megoldását!

Hogyan változnak a harmonikus rezgések kinetikai és potenciális energiái az idő múlásával? Miért marad állandó egy harmonikus rezgés összenergiája?

Vezess le egy differenciálegyenletet, amely leírja a csillapított rezgéseket, és írja fel a megoldását!

Mi a logaritmikus csillapítás csökkenése?

Mi a rezonancia? Rajzolja fel a kényszerrezgések amplitúdóját a hajtóerő frekvenciájának függvényében, ha ez az erő az idő egyszerű harmonikus függvénye.

Mik azok az önrezgések? Mondjon példákat önrezgésekre!

5. FÜGGELÉK

teszt a „Mechanikai rezgések” témában

Merev test, rugóval felfüggesztve

Súlytalan, nyújthatatlan menetre felfüggesztett anyagi pont

Súlytalan, nyújthatatlan menetre felfüggesztett merev test

Bármely merev test, amely egyensúlyi helyzete körül rezeg

Ugyanabban a fázisban oszcilláló pontok geometriai helye

Különböző fázisokkal oszcilláló pontok geometriai helye

Azoknak a pontoknak a geometriai elhelyezkedése, amelyekhez a rezgések a t időpontban érnek

Hullámfelületi pontok geometriai helye

Maximális periódusérték

Az ingadozó mennyiség maximális értéke

Az a maximális frekvenciaérték, amelynél rezonancia lép fel

Az ingadozó mennyiség minimális értéke

Oszcillációk, amelyek az eredetileg átadott energia miatt következnek be, és egy későbbi hiány külső hatások az oszcillációs rendszerhez

Az oszcillációs rendszert érő külső hatások energiája miatt fellépő rezgések

4) A természetben fellelhető bármilyen rezgés

A természetben fellelhető bármilyen rezgés

Olyan folyamatok, amelyeket bizonyos időbeli ismételhetőség jellemez

Oszcillációk, amelyekben az ingadozó mennyiség idővel változik a szinusz vagy koszinusz törvénye szerint

A külső hatások összenergiája és a rendszer természetes oszcillációi miatt fellépő rezgések

Az az idő, amely alatt egy teljes oszcilláció következik be

A t idő alatt végrehajtott teljes oszcillációk teljes száma

A negyed oszcilláció befejezéséhez szükséges idő

Az időegység alatt végrehajtott teljes oszcillációk száma

Az az idő, amely alatt az oszcillációk teljesen lecsengenek

Egy teljes oszcilláció ideje

Egyenlő érték kölcsönös szám ingadozások

Az egymást követő amplitúdók arányának logaritmusa

A szinusz vagy koszinusz előjel alatti mennyiség és az oszcillációs periódus pillanatnyi értékének meghatározása

A szinusz vagy koszinusz jel alatti mennyiség, amely meghatározza a teljes rezgés időtartamát

Olyan mennyiség, amely a szinusz vagy koszinusz előjel alatt áll, és meghatározza az oszcillációs rendszer pillanatnyi állapotát.

A szinusz vagy koszinusz előjel alatti mennyiség és az egyensúlyi helyzettől való maximális eltérés meghatározása

Csökken

Növeli

Nem változik

Kissé változik

A gyakoriságok egyenlőek

A csillapítatlan rezgések gyakorisága kisebb

A csillapított rezgések gyakorisága kisebb

A csillapított rezgések gyakorisága nagyobb

Lineáris

A koszinusz törvénye szerint

Kvadratikusan

Exponenciális

A teljes inga hossza

Annak a matematikai inga hossza, amelynek rezgési periódusa megegyezik egy fizikai inga lengésperiódusával

A matematikai inga hossza

1/2 matematikai inga hosszának

Ibolya

Ibolya

Az elmozdulás időfüggősége

A sebesség időfüggősége

A mozgási energia időfüggősége

A potenciális energia időfüggősége

Az elmozdulás grafikonja az idő függvényében

Sebesség-idő grafikon

Az elmozdulás és a sebesség grafikonja

A teljes energia grafikonja az idő függvényében

Harmonikus csillapítás

Harmonikus folytonos

Nem harmonikus csillapítás

Nem harmonikus folyamatos

Válaszok a „Mechanikai rezgések” tesztre

Szám
kérdés

Szám
helyes válasz

Szám
kérdés

Szám
helyes válasz

Szám
kérdés

Szám
helyes válasz

3) Szárazföldi reakcióerő _________________________________________________________________________________________________________________________________________________________________________________________________________

4) N = ____________________

5) Súrlódási együttható - _____________________________________________________________________________________________________________________________________________________________________________________________________________

6) µ=_________________________

7) Maximális dőlésszög (maximális szög), α max __________________________________________________

8) Gyorsulás, a=___________________________________________________

Helyezze a vezérlőket tetszőleges pozícióba, és rögzítse a kezdeti adatokat a táblázatban.
Nyomja meg a "Start" gombot, és figyelje a sáv mozgását
Írja fel a súrlódási erő, a támasztó reakcióerő, a testgyorsulás értékét, amely a modell munkaterületén található kijelzőn található.
Számítsa ki a súrlódási erőt, a támasztó reakcióerőt, a test gyorsulását, valamint a sík maximális dőlésszögét.

Dőlésszög, α, fok

Súrlódási együttható,
µ

m, kg

A modell által számított értékek

A tanuló által számított értékek

Határszög, α max

Súrlódási erő, F tr, N

Gyorsulás, m/s 2

Földi reakcióerő, N, N

Súrlódási erő, F tr, N

Gyorsulás, m/s 2

Földi reakcióerő, N, N

Ábrázoljuk a sebességet az idő függvényében V (t):

Következtetés_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Számítógépes kísérlet Számítógépes kísérlet Az új tervezési fejlesztések életre keltéséhez, új műszaki megoldások gyártásba való bevezetéséhez vagy új ötletek teszteléséhez kísérletre van szükség. A közelmúltban egy ilyen kísérletet akár laboratóriumi körülmények között, speciálisan erre kialakított létesítményeken, akár in situ, pl. a termék valódi mintáján, mindenféle vizsgálatnak alávetve. Ez nagy anyagköltséget és időt igényel. A modellek számítógépes tanulmányozása segített. Számítógépes kísérlet során a modellek helyességét ellenőrzik. A modell viselkedését különféle objektumparaméterek mellett tanulmányozzuk. Minden kísérlethez az eredmények megértése társul. Ha a számítógépes kísérlet eredményei ellentmondanak a megoldandó probléma jelentésének, akkor a hibát egy rosszul megválasztott modellben vagy a megoldási algoritmusban és módszerben kell keresni. A hibák azonosítása és kiküszöbölése után a számítógépes kísérlet megismétlődik. Ahhoz, hogy életet adjunk az új tervezési fejlesztéseknek, új műszaki megoldásokat vigyünk be a gyártásba, vagy új ötleteket teszteljünk, kísérletre van szükség. A közelmúltban egy ilyen kísérletet akár laboratóriumi körülmények között, speciálisan erre kialakított létesítményeken, akár in situ, pl. a termék valódi mintáján, mindenféle vizsgálatnak alávetve. Ez nagy anyagköltséget és időt igényel. A modellek számítógépes tanulmányozása segített. Számítógépes kísérlet során a modellek helyességét ellenőrzik. A modell viselkedését különféle objektumparaméterek mellett tanulmányozzuk. Minden kísérlethez az eredmények megértése társul. Ha a számítógépes kísérlet eredményei ellentmondanak a megoldandó probléma jelentésének, akkor a hibát egy rosszul megválasztott modellben vagy a megoldási algoritmusban és módszerben kell keresni. A hibák azonosítása és kiküszöbölése után a számítógépes kísérlet megismétlődik.

A matematikai modellen képletek, egyenlőtlenségek stb. matematikai összefüggéseinek rendszerét értjük, amelyek tükrözik egy objektum vagy folyamat lényeges tulajdonságait. A matematikai modellen képletek, egyenlőtlenségek stb. matematikai összefüggéseinek rendszerét értjük, amelyek tükrözik egy objektum vagy folyamat lényeges tulajdonságait.

Problémák modellezése különböző tantárgyakból Problémák modellezése különböző tantárgyakból Közgazdaságtan Közgazdaságtan Közgazdaságtan Csillagászat Csillagászat Csillagászat Csillagászat Fizika Fizika Fizika Ökológia Ökológia Ökológia Biológia Biológia Biológia Földrajz Földrajz Földrajz

A termékeket kialkudott áron értékesítő gépgyártó bizonyos bevételhez jutott, mivel bizonyos összeget költött a termelésre. Határozza meg a nettó nyereség és a befektetett források arányát! A termékeket kialkudott áron értékesítő gépgyártó bizonyos bevételhez jutott, mivel bizonyos összeget költött a termelésre. Határozza meg a nettó nyereség és a befektetett források arányát! Probléma megfogalmazása Probléma megfogalmazása A szimuláció célja a termékek gyártási és értékesítési folyamatának tanulmányozása a legnagyobb nettó profit elérése érdekében. Közgazdasági képletek segítségével keresse meg a nettó nyereség és a befektetett források arányát! A modellezés célja a termékek gyártási és értékesítési folyamatának feltárása a legnagyobb nettó profit elérése érdekében. Közgazdasági képletek segítségével keresse meg a nettó nyereség és a befektetett források arányát!

A modellezési objektum fő paraméterei: bevétel, költség, nyereség, jövedelmezőség, nyereségadó. A modellezési objektum fő paraméterei: bevétel, költség, nyereség, jövedelmezőség, nyereségadó. Bemenő adatok: Bemenő adatok: bevétel B; bevétel B; költségek (költség) S. költségek (költség) S. Az alapvető gazdasági függőségek segítségével további paramétereket fogunk találni. A nyereség értékét a bevétel és a költség különbségeként határozzuk meg P=B-S. A többi paramétert az alapvető gazdasági függőségek segítségével találjuk meg. A nyereség értékét a bevétel és a költség különbségeként határozzuk meg P=B-S. Az r jövedelmezőséget a következő képlettel számítjuk ki:. Az r jövedelmezőséget a következő képlettel számítjuk ki:. Az 50%-os jövedelmezőség határszintjének megfelelő nyereség az S előállítási költség 50%-a, azaz. S*50/100=S/2, ezért az N nyereségadót a következőképpen határozzuk meg: Az 50%-os jövedelmezőségi határszintnek megfelelő nyereség az S előállítási költség 50%-a, azaz. S*50/100=S/2, tehát az N nyereségadót a következőképpen határozzuk meg: ha r

Eredmények elemzése Eredmények elemzése A kapott modell lehetővé teszi a nyereségesség függvényében a nyereségadó meghatározását, a nettó nyereség összegének automatikus újraszámítását, valamint a nettó nyereség és a befektetett források arányának meghatározását. Az így kapott modell lehetővé teszi a nyereségességtől függően a nyereségadó meghatározását, a nettó nyereség összegének automatikus újraszámítását, valamint a nettó nyereség és a befektetett pénzeszközök arányának meghatározását. Egy számítógépes kísérlet azt mutatja, hogy a nettó nyereség és a befektetett forrás aránya a bevétel növekedésével nő, és csökken a termelési költségek növekedésével. Egy számítógépes kísérlet azt mutatja, hogy a nettó nyereség és a befektetett forrás aránya a bevétel növekedésével nő, és csökken a termelési költségek növekedésével.

Feladat. Feladat. Határozza meg a pályán keringő bolygók sebességét! Ehhez hozzon létre egy számítógépes modellt Naprendszer. A feladat megfogalmazása A szimuláció célja a keringő bolygók sebességének meghatározása. Modellező objektum: Naprendszer, melynek elemei bolygók. Belső szerkezet a bolygókat nem veszik figyelembe. A bolygókat a következő jellemzőkkel rendelkező elemeknek tekintjük: név; R - távolság a Naptól (csillagászati egységekben; csillagászati egységekben. átlagos távolság a Földtől a Napig); t a Nap körüli forradalom időszaka (években); V a keringési sebesség (asztroegység/év), feltételezve, hogy a bolygók állandó sebességgel körben keringenek a Nap körül.

Eredmények elemzése Eredmények elemzése 1. Elemezze a számítási eredményeket. Lehetséges azt mondani, hogy a Naphoz közelebb elhelyezkedő bolygók keringési sebessége nagyobb? 1. Elemezze a számítási eredményeket. Lehetséges azt mondani, hogy a Naphoz közelebb elhelyezkedő bolygók keringési sebessége nagyobb? 2. A Naprendszer bemutatott modellje statikus. A modell megalkotásakor figyelmen kívül hagytuk a bolygók és a Nap közötti távolság változásait keringési mozgásuk során. Ez az információ elég ahhoz, hogy megtudjuk, melyik bolygó van távolabb, és mi a hozzávetőleges kapcsolat a távolságok között. Ha meg akarjuk határozni a Föld és a Mars távolságát, akkor nem hagyhatjuk figyelmen kívül az átmeneti változásokat, és itt egy dinamikus modellt kell használnunk. 2. A Naprendszer bemutatott modellje statikus. A modell megalkotásakor figyelmen kívül hagytuk a bolygók és a Nap közötti távolság változásait keringési mozgásuk során. Ez az információ elég ahhoz, hogy megtudjuk, melyik bolygó van távolabb, és mi a hozzávetőleges kapcsolat a távolságok között. Ha meg akarjuk határozni a Föld és a Mars távolságát, akkor nem hagyhatjuk figyelmen kívül az átmeneti változásokat, és itt egy dinamikus modellt kell használnunk.

Számítógépes kísérlet Írja be a kezdeti adatokat a számítógépes modellbe. (Például: =0,5; =12) Határozza meg azt a súrlódási együtthatót, amellyel az autó lemegy a hegyről (adott szögben). Keresse meg azt a szöget, amelyben az autó a hegyen fog állni (adott súrlódási együttható mellett). Mi lesz az eredmény, ha a súrlódási erőt figyelmen kívül hagyjuk? Az eredmények elemzése Ez a számítógépes modell lehetővé teszi, hogy fizikai kísérlet helyett számítási kísérletet végezzen. A forrásadatok értékeinek megváltoztatásával láthatja a rendszerben bekövetkező összes változást. Érdekes megjegyezni, hogy a megépített modellben az eredmény nem függ sem az autó tömegétől, sem a gravitációs gyorsulástól.

Feladat. Feladat. Képzeld el, hogy csak egy édesvízforrás marad a Földön, a Bajkál-tó. Hány évig biztosítja a Bajkál vízzel az egész világ lakosságát? Képzeld el, hogy csak egy édesvízforrás marad a Földön, a Bajkál-tó. Hány évig biztosítja a Bajkál vízzel az egész világ lakosságát?

Modellfejlesztés Modellfejlesztés A matematikai modell felépítéséhez meghatározzuk a kiindulási adatokat. Jelöljük: A matematikai modell felépítéséhez definiáljuk a kiindulási adatokat. Jelöljük: V - a Bajkál-tó térfogata km3; V a Bajkál-tó térfogata km3; N - Föld lakossága 6 milliárd ember; N - Föld lakossága 6 milliárd ember; p - napi vízfogyasztás személyenként (átlagosan) 300 l. p - napi vízfogyasztás személyenként (átlagosan) 300 l. 1l óta. = 1 dm3 víz, a tó vizének V-jét km3-ről dm3-re kell átalakítani. V (km3) = V * 109 (m3) = V * 1012 (dm3) 1l óta. = 1 dm3 víz, a tó vizének V-jét km3-ről dm3-re kell átalakítani. V (km3) = V * 109 (m3) = V * 1012 (dm3) Az eredmény azoknak az éveknek a száma, amelyek során a Föld lakossága használja a Bajkál-tó vizét, jelöljük g-vel. Tehát g=(V*)/(N*p*365) Az eredmény az, hogy hány év alatt használja a Föld lakossága a Bajkál-tó vizét, jelöljük g-vel. Tehát g=(V*)/(N*p*365) Így néz ki a táblázat képletmegjelenítési módban: Így néz ki a táblázat képletmegjelenítési módban:

Feladat. Feladat. A vakcina előállításához a tervek szerint baktériumkultúrát termesztenek az üzemben. Ismeretes, hogy ha a baktériumok tömege x g, akkor egy nap után (a-bx)x g-val nő, ahol az a és b együttható a baktérium típusától függ. Az üzem naponta m baktériumot fog gyűjteni vakcinagyártáshoz. A terv elkészítéséhez fontos tudni, hogyan változik a baktériumok tömege 1, 2, 3,..., 30 nap elteltével A vakcina előállításához baktériumtenyészet termesztését tervezik az üzemben. Ismeretes, hogy ha a baktériumok tömege x g, akkor egy nap után (a-bx)x g-val nő, ahol az a és b együttható a baktérium típusától függ. Az üzem naponta m baktériumot fog gyűjteni vakcinagyártáshoz. A terv elkészítéséhez fontos tudni, hogyan változik a baktériumok tömege 1, 2, 3,..., 30 nap után.

Probléma megfogalmazása Probléma megfogalmazása A modellezés tárgya a népesség időtől függő változási folyamata. Ezt a folyamatot számos tényező befolyásolja: a környezet, az egészségügyi ellátás állapota, az ország gazdasági helyzete, a nemzetközi helyzet és még sok más. A demográfiai adatok összegzése után a tudósok levezettek egy függvényt, amely kifejezi a populáció időfüggőségét: A modellezés tárgya a populáció időtől függő változásának folyamata. Ezt a folyamatot számos tényező befolyásolja: a környezet, az egészségügyi ellátás állapota, az ország gazdasági helyzete, a nemzetközi helyzet és még sok más. A demográfiai adatok általánosítása után a tudósok levezettek egy függvényt, amely kifejezi a népesség időfüggőségét: f(t)=ahol az a és b együtthatók eltérőek az egyes állapotokban, f(t)=ahol az a és b együtthatók eltérőek minden állapot, e a természetes logaritmus alapja. e a természetes logaritmus alapja. Ez a képlet csak megközelítőleg tükrözi a valóságot. Az a és b együtthatók értékének megtalálásához használhat statisztikai referenciakönyvet. A referenciakönyvből az f(t) értékeket (populáció mérete t időpontban) figyelembe véve megközelítőleg kiválaszthatja a-t és b-t úgy, hogy a képlettel számított f(t) elméleti értékei ne sokban térjenek el a tényleges adatok a referenciakönyvben. Ez a képlet csak megközelítőleg tükrözi a valóságot. Az a és b együtthatók értékének megtalálásához használhat statisztikai referenciakönyvet. A referenciakönyvből az f(t) értékeket (populáció mérete t időpontban) figyelembe véve megközelítőleg kiválaszthatja a-t és b-t úgy, hogy a képlettel számított f(t) elméleti értékei ne sokban térjenek el a tényleges adatok a referenciakönyvben.

A számítógép, mint oktatási tevékenység eszköze lehetővé teszi a természettudományok számos kérdésének tanulmányozásában a hagyományos megközelítések újragondolását, a tanulók kísérleti tevékenységének erősítését, valamint a tanulási folyamat közelítését a modellezésen alapuló megismerés valódi folyamatához. technológia. A számítógép, mint oktatási tevékenység eszköze lehetővé teszi a természettudományok számos kérdésének tanulmányozásában a hagyományos megközelítések újragondolását, a tanulók kísérleti tevékenységének erősítését, valamint a tanulási folyamat közelítését a modellezésen alapuló megismerés valódi folyamatához. technológia. Az emberi tevékenység különböző területein felmerülő problémák számítógépen történő megoldása nemcsak a modellezési technológiai tudáson alapul, hanem természetesen ennek ismeretén is. tárgykörben. Ebben a tekintetben célszerűbb a javasolt modellezési órákat azután lebonyolítani, hogy a tanulók elsajátították a tananyagot egy közismereti tantárgyból, az informatika tanárnak együtt kell működnie különböző szakok tanáraival. oktatási területeken. Ismert tapasztalat van a bináris leckék levezetésében, pl. az informatika tanár és a szaktanárral közösen tartott órákat. Az emberi tevékenység különböző területeiből származó problémák számítógépen történő megoldása nem csak a modellezési technológiai ismereteken alapul, hanem természetesen egy adott tantárgy ismeretén is. Ebben a tekintetben célszerűbb a javasolt modellezési órákat azután lefolytatni, hogy a tanulók elsajátították a tananyagot egy közismereti tantárgyból, az informatika tanárnak együtt kell működnie különböző oktatási területek tanáraival. Ismert tapasztalat van a bináris leckék levezetésében, pl. az informatika tanár és a szaktanárral közösen tartott órákat.

Fizikai modellek tanulmányozása Készítette: Kukleva Anastasia

A modellezés egy rendszer tanulmányozásának eszköze úgy, hogy azt egy kényelmesebb kutatási rendszerrel (modellel) helyettesítjük, amely megőrzi a kutatót érdeklő tulajdonságokat. A modellezés a modellek felépítése (vagy kiválasztása) és tanulmányozása annak érdekében, hogy új ismereteket szerezzenek az objektumokról. A modell bármilyen természetű objektum, amely képes helyettesíteni a vizsgált objektumot a kutatót érdeklő tulajdonságokban (például a földgömb a Föld modellje). Az objektum leírása – információkészlet a vizsgált rendszerről és azokról a feltételekről, amelyek mellett a vizsgálatot el kell végezni.

Osztályozás (V.A. Venikov javaslata) Logikai modellek A logikai modelleket érvelés alapján hozzuk létre. Bármelyik személy, mielőtt bármit megtenne, felállít egy logikai modellt. A logikai modell hűsége az időt mutatja. Az általunk ismert ilyen típusú modelleket nem mindig erősítették meg. A logikai modellek előnye, hogy jelen vannak minden más típusú modellben. Fizikai modellek A valós rendszerhez fizikailag hasonló modellek. A fizikai modellek közötti fő különbség a vizsgált legfontosabb tulajdonságok fizikai hasonlósága. A fizikai modellek legszembetűnőbb példái a gyermekjátékok. Egy másik példa egy autó tervezése során a tervezők egy gyurmából készült fizikai modellt építenek a jövőbeli termékről. Az ilyen típusú modellek előnye az eredmények legmagasabb fokú tisztasága. Matematikai modellek A matematikai modell a vizsgált rendszer szigorúan formalizált leírása a matematika nyelvén. Az előny a szigorúan formalizált bizonyítékok és a kapott eredmények érvényessége. (például rendszer lineáris egyenletek- megoldási módszer). Ez a fajta modellezés jelenleg meghatározó a rendszerkutatásban. Szimulációs (számítógépes) modellezés A szimulációs modellezés numerikus kísérlet a vizsgált rendszer elemeinek matematikai modelljeivel, információs szinten kombinálva. A szimulációs modellek nemcsak a vizsgált rendszer elemeinek matematikai modelljeit tartalmazhatják, hanem fizikai modelleket is. (például szimulátor).

Fizikai modellek tanulmányozása. A gravitáció hatása alatti mozgás jól ismert. Ez egy test leesése egy bizonyos magasságból, és a horizonthoz képest szögben elvetett test mozgása stb. Ha ilyen problémáknál a légellenállás erejét nem vesszük figyelembe, akkor az összes felsorolt mozgástípust jól ismert képletekkel írjuk le. De nem kevésbé érdekesek azok a problémák, amelyekben a légellenállást figyelembe veszik.

Feladat Egy ejtőernyős mozgása.

I. szakasz. A probléma megfogalmazása A PROBLÉMA LEÍRÁSA A földre zuhanáskor az ejtőernyős a gravitáció és a légellenállás hatását tapasztalja. Kísérletileg megállapították, hogy az ellenállási erő a mozgás sebességétől függ: minél nagyobb a sebesség, annál nagyobb az erő. A levegőben való mozgás során ez az erő arányos a sebesség négyzetével egy bizonyos k ellenállási együttható mellett, ami az ejtőernyő kialakításától és az ember súlyától függ. Mekkora legyen ennek az együtthatónak az értéke ahhoz, hogy az ejtőernyős 8 m/s-nál nem nagyobb sebességgel szálljon le a földre, ami nem jelent egészségügyi veszélyt? Határozza meg a modellezés céljait és formalizálja a problémát.

szakasz II. Modellfejlesztés INFORMÁCIÓS MODELL Hozzon létre saját információs modellt. MATEMATIKAI MODELL Az ábrán az ejtőernyősre ható erők láthatók. Newton második törvénye szerint az erők hatására bekövetkező mozgás egyenlőségnek írható fel.

Ezt az egyenlőséget a mozgás tengelyére vetítjük, a légellenállási erő kifejezést behelyettesítjük, így kapunk egy képletet a gyorsulás kiszámításához

Kiszámoljuk az ejtőernyős által megtett sebességet és távolságot egyenlő időközönként Δt. Az időpillanatok kiszámításának képlete a következő: ti+1=ti+Δt Azt is feltételezzük, hogy minden intervallumban a gyorsulás állandó és egyenlő ai-vel. A gyorsulás kiszámításának képlete: ahol Vi a sebesség az intervallum elején (V0 a kezdeti sebesség).

A sebességet az intervallum végén (és ennek megfelelően a következő elején) az egyenletesen gyorsított mozgás képletével számítjuk ki.Az ejtőernyős által megtett távolság egyenlő a megtett távolság összegével. a következő időintervallumot és az ezen intervallum alatt megtett távolságot.

SZÁMÍTÓGÉPES MODELL A modellezéshez táblázatkezelő környezetet választunk. Ebben a környezetben az információs és a matematikai modell egy táblázatban egyesül, amely három területet tartalmaz: forrásadatok; közbenső számítások; eredmények.

szakasz III. Számítógépes kísérlet

Formális modell A modell formalizálásához a fizika tantárgyból ismert egyenletes és egyenletesen gyorsított mozgás képleteit használjuk.

Köszönöm a figyelmet!!!

Fizikai modellek tanulmányozása. A számítógépes interaktív modellek fizikaórákon való használatának koncepciója „Mechanikai rezgések” és „Testek mozgása több erő hatására” óravázlat

BEVEZETÉS

1 A kísérlet számítógépes szimulációja

1.1 Az elektronikus média használatának előnyei és hátrányai

2Virtuális modellek használata a fizika tanulmányozásában

2.1 Matematikai inga

2.1.1 Harmonikus rezgések és jellemzőik

2.1.2 Csillapított harmonikus rezgések

2.1.3 Harmonikus rezgések energiája

2.2 Fizikai inga

2.3 Blokkolás ferde síkon

2.4 Két test egy ferde síkban

3 Gyakorlati gyakorlatok

3.1.1 Laboratóriumi feladat

3.1.2 Hozzárendelés a matematikai ingamodellhez

3.1.3 „Mechanikai rezgések” teszt

3.1.4 „Mechanikai rezgések” és „Testek mozgása több erő hatására” leckék vázlata

3.1.5 Gyakorlatorientált feladatok

KÖVETKEZTETÉS

A HASZNÁLT FORRÁSOK LISTÁJA

1. MELLÉKLET

2. MELLÉKLET

3. FÜGGELÉK

4. FÜGGELÉK

5. FÜGGELÉK